Podstawowe pojęcia i narzędzia informatyki

Zajęcia 2

Teoria informacji *

Kompresja

Do czego wykorzystywanie jest kodowanie (w nawiasie podane wielkość surowych, nieskompresowanych danych):

tekst (1000 stron - 5MB)

audio (30 sek. - 5,3 MB)

video (minuta - 1.416 GB)

obraz (512x512 pikseli - 0,786 MB)

Celem kompresji jest reprezentowanie sygnałów (danych) w bardziej wydajnej formie. Kompresja jest użyteczna zarówno z punktu widzenia transmisji jak przechowywania danych.

Podstawową ideą kompresji jest wykorzystanie resundancji w danych.

Załóżmy, że mamy $M$ symboli $s_1,s_2...,s_M$. Chcemy zapisać symbole za pomocą bitów ($0$ i $1$). Ciąg bitów odpowiadający danemu symbolowi nazwiemy słowem kodowym. Problem kodowania to przyporządkowanie każdemu z symboli $s_1,s_2...,s_M$ słowa kodowego korzystając z możliwie najmniejszej liczby bitów.

Ile bitów potrzebujemy aby to osiągnąć? Odpowiedź to oczywiście $\log_2M$.

Np dla $8$ symboli $s_1,s_2...,s_8$ musimy użyć słów kodowych $000, 001, 010, 011, 100, 101, 110, 111$. Dla $26$ liter, $\log_{2}26 \approx 4.7$, co oznacza, że potrzebujemy $5$ symboli.

Bez dodatkowych założeń nie możemy zakodować niczego lepiej niż za pomocą $\log_2M$ bitów. Co jednak gdy mamy dokładniejsze informacje na temat danych, np. wiemy że pewne symbole (struktury) występują częściej?

Kody o zmiennej długości słowa

W przypadku częściej występujących znaków stosujemy krótsze słowa kodowe. Np. wykorzystane przez Morse'a w kodowaniu Morsa poprzez dopasowanie do częstotliwości występowania liter w Angielskich słowach.

Inny przykład: mając $4$ symbole możemy je zakodować na dwóch bitach przez $00,01,10,11$. Co jednak, gdy wiemy, że prawdopodobieństwo wystąpienia symbolu $s_1$ wynosi $\frac{1}{2}$, symbolu $s_2$ wynosi $\frac{1}{4}$, a symboli $s_3,s_4$ wynosi $\frac{1}{8}$. Możemy przyporządkować symbolom słowa kodowe $0,10,110,111$. Możemy wyliczyć średnią liczbę symboli jakie wykorzystamy w kodowaniu:

\begin{equation*} (1)(1/2) + (2)(1/4) + (3)(1/8) + (3)(1/8) = 1.75 \end{equation*}

Oznacza to, że średnio żeby zakodować jeden symbol wykorzystamy $1.75$ bitów, a nie $2$ bity. W związku z tym np. nasz plik zamiast $2$ MB może zajmować $1.75$ MB.

Dlaczego wybraliśmy takie słowa, a nie inne? Odpowiedź na to pytanie jest taka, że musimy móc określić jednoznacznie kiedy kończy się jedno słowo a kiedy zaczyna kolejne. Załóżmy, że do kodowania użyjemy słów $0,10,01,11$, wtedy dla ciągu $0110$ nie jesteśmy w stanie odróżnić, czy chodziło o ciąg $s_3,s_2$ czy też o $s_1s_4s_1$. Pokazuje to, że słowo nie jest unikalnie odkodowywalne.

Kody prefix-free (jednoznaczny)

Kod nazywamy prefix-free jeżeli żande ze słów kodowych nie jest prefiksem innego. Wyżej wymieniony kod był prefix-free. Następujęcy kod nie jest: $(0,01,011,111)$, przez co musimy odczytać wszystkie bity żeby odkodować dane, a nie możemy tego robić online (np. dla wpisu $011111...1$ do ostatniego bitu nie wiemy, co było na początku).

Projektowanie kodowania

Formalnie w teorii informacji stosujemy nazewnictwo wzięte z teorii komunikacji, w związku z tym mówimy o tym jak dużo informacji niesie ze sobą informacja (komunikat), i tak im bardziej zaskakujący jest komunikat, tym więcej niesie ze sobą informacji.

W szczególności jeżeli zdarzenie ma prawdopodobieństwo $1$ to jest ono pewne. Nie ma żadnej niespodzianki w tym, że dane zdarzenie zaszło i w związku z tym jego zajście nie niesie ze sobą żadnej informacji. Z drugiej strony dla zdarzeń o prawdopodobieństwo bliskim $0$, ich wystąpienie jest dużym zaskoczeniem, w tym wypadku otrzymujemy dużo informacji dowiadując się, że ono zaszło. W przypadku zdarzeń o prawdopodobieństwie $\frac{1}{2}$ otrzymujemy dokładnie $1$ bit informacji dowiadując się że zdarzenie zaszło.

Ilość informacji uzyskanych przez wystąpienie danego zdarzenia jest odwrotnie proporcjonalne do prawdopodobieństwa jego wystąpienia. Formalnie stosujemy następującą miarę:

\begin{equation*} \text{ilość informacji uzyskana przy wystąpieniu zdarzenia o prawdopodobieństwie } p = \log_{2}\frac{1}{p} \text{ bitów} \end{equation*}

W naszych rozważaniach założymy, że z symbolami $s_1,s_2...,s_M$ związany jest wektor prawdopodobieństw $p_1,p_2...,p_M$, gdzie $0\leq p_i \leq 1$ dla każdego $i$ oraz $p_1+p_2+...+p_m = 1$. Ponadto symbole pojawiają się na wejściu losowane niezależnie z rozkładem zadanym przez wspomniany wcześniej wektor prawdopodobieństw.

W zwiazku z tym średnia liczna bitów informacji uzyskiwanych od źródła na wejściu jest obliczana ze wzoru

\begin{equation*} p_1 \log_{2}\frac{1}{p_1} + ... + p_M \log_{2}\frac{1}{p_M} = \sum_{i=1}^{M} p_i \log_{2}\frac{1}{p_i} \end{equation*}

i nazywamy entropią.

Entropia

Zazwyczaj entropię oznaczamy przez $H$.

\begin{equation*} H = \sum_{i=1}^{M} p_i \log_{2}\frac{1}{p_i} \end{equation*}

Twierdzenie Shannona z 1948 mówi o tym, że każdy unikalnie odkodowywalny kod musi używać średnio co najmniej $H$ bitów na jeden symbol. Nie istnieje lepsze kodowanie.

Kodowanie Huffmana

Jeżeli znamy wektor prawdopodobieństw występowania symboli na wejściu, wtedy jedną z metod uzyskiwania wydajnego kodowania jest tzw. Kodowanie Huffmana. Otrzymane kodowanie jest unikalnie dekodowalne i prefix-free. Wykorzystuje się je w kodowaniach np. JPEG, czy MPEG.

Algorytm:

Traktujemy prawdopodobieństwa jako liście drzewa.

Tworzymy drzewo w następujący sposób: łączymy dwa wierzchołki o najmniejszych prawdopodobieństwach rodzicem, przypisujemy jednej z nowo powstałych krawędzi $1$ a drugiej $0$.

Słowo kodowe danego symbolu jest wyznaczone przez ścieżkę od korzenia do liścia w którym znajduje się ten symbol.

Przykład:

Weźmy $4$ symbole $s_1,s_2,s_3,s_4$ o prawdopodobieństwach $1/2,1/4,1/8,1/8$, kod Huffmana jest tworzony następująco:

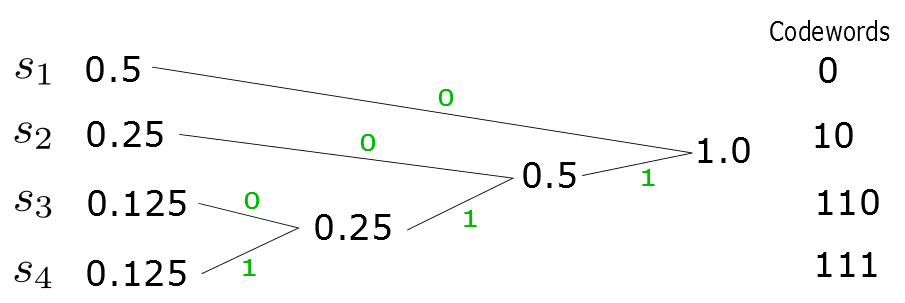
Otrzymaliśmy w tym przypadku takie same kodowanie jak w podanym wcześniej przypadku. Średnia liczba bitów na symbol wynosi więc w tym wypadku $1.75$.

Jaka jest optymalna wartość jaką możemy w tym wypadku uzyskać? Licząc entropię mamy:

\begin{equation*} \begin{array}{ccl} H & = & \frac{1}{2} \log_22 + \frac{1}{4}\log_24 + \frac{1}{8}\log_28 + \frac{1}{8}\log_28 \\ & = & \frac{1}{2} + \frac{1}{2} + \frac{3}{8} + \frac{3}{8} \\ & = & 1.75\\ \end{array} \end{equation*}

Wynika stąd, że kod Huffmana jest w tym wypadku optymalny. W ogólności można udowodnić, że

\begin{equation*} H \leq \text{ średnia długość kodu Huffmana } \leq H+1 \end{equation*}

Wadami kodów Huffmana są:

Konieczność określenia prawdopodobieństw występienia poszczególnych symboli oraz założenie o ich niezależnośći względem siebie.

Propagacja błędów (w odróżnieniu od kodów o stałej licznie znaków).

Redundancja

Różnicę między średnią długością kodu Huffmana a entropią nazywamy redundancją kodu.

Kod zwarty

Kodem zwartym nazywamy kod jednoznaczny o minimalnej redundancji.

Zadanie 1

Znajdź kod Huffmana dla prawdopodobieństw $0.25,0.21,0.15,0.14,0.0625,0.0625,0.0625,0.0625$ oraz oblicz dla niego średnią ilość bitów na symbol, porównaj tę wartość z entropią.

Zadanie 2

Żródło wysyła 6 komunikatów z prawdopodobieństwami i kodami:

P(s1) = 5/16, kod: 00

P(s2) = 5/16, kod: 01

P(s3) = 3/16, kod: 10

P(s4) = 1/16, kod: 110

P(s5) = 1/16, kod: 1110

P(s6) = 1/16, kod: 1111

Oblicz redundancję tego kodu? Czy kod jest jednoznaczny?

Zadanie 3

Dla zbioru 7 symboli o prawdopodobieństwach: $1/3, 1/3, 1/9, 1/9, 1/27, 1/27, 1/27$ podać kod zwarty i kod o minimalnej równej długości słów kodowych.

Zadanie Domowe Punktowane - 10 pkt

Dokonaj kompresji metodą Huffmana zakładając, że źródło danych emituje podane symbole z równym prawdopodobieństwem:

Litery twojego imienia i nazwiska

e c e c n n b b e a d e

m e n b b b d a e n a m

np. Dla Marcin Witkowski będą to symbole

m a r c i n w i t k o w s k i

e c e c n n b b e a d e

m e n b b b d a e n a m

Odpowiedz na pytania:

Ile różnych symboli emituje źródło?

Podaj sumaryczne prawdopodobieństwa wystąpień symboli.

Podaj kod Huffmana dla tego źródła.

Oblicz i podaj entropię źródła oraz redundancję.

Termin wykonania zadania: Sobota 17(lub 24).10.2015 do godziny 24.00. Proszę o przesłanie rozwiązań mailem lub dostarczenie osobiście. W rozwiązaniu należy podać (pokazać) kolejne kroki dochodzenia do rozwiązania. Odpowiedzią może być zdjęcie kartki z rozwiązaniem (byleby załącznik miał sensowny rozmiar).

W tytule wiadomości musi się znaleźć słowo DNIF oraz numer indeksu. Za każdy kolejny tydzień opóźnienia oddania zadania ocena za zadanie zostaje pomniejszona o 15%.

*: Wykorzystano materiały z

https://www.princeton.edu/~cuff/ele201/kulkarni_text/information.pdf